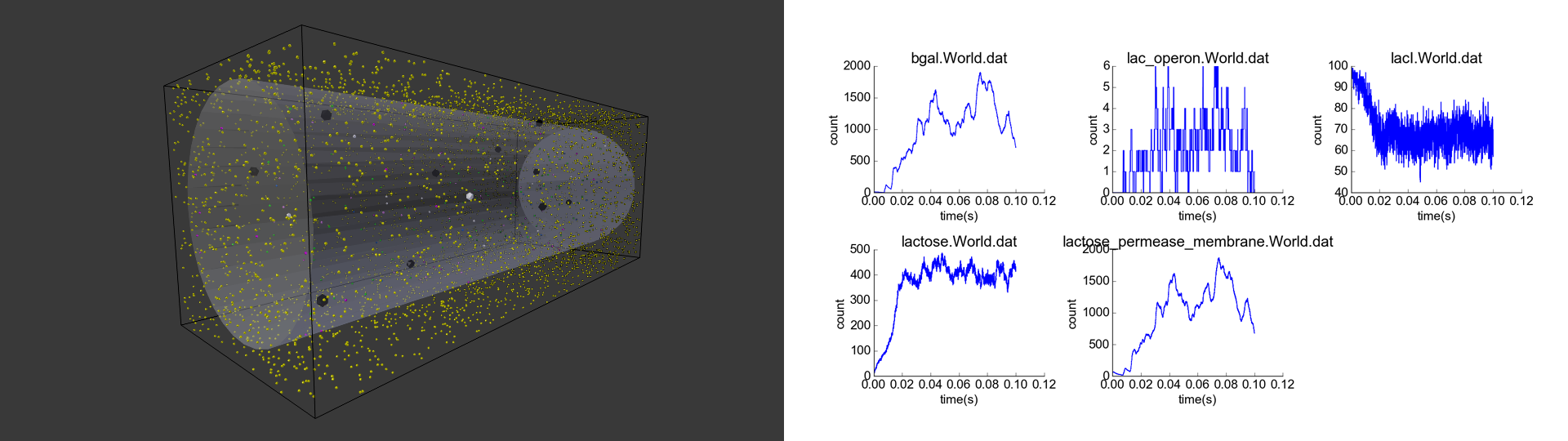
I did this project for the CS 279 course (Computational Biology: Structure and Organization of Cells) in Fall 2015. In this class, I learned about priciples and algorithms for applying computation to the study of structure and dynamics from the molecular level to the cellular level. For the final project, I chose to investigate in depth one topic covered in the course, namely spatial stochastic (particle-based) reaction-diffusion simulations of particles.
Report Summary
Mathematical and computational modeling of the dynamics of biological systems, ranging in complexity from genetic circuits to entire cells, is an active area of research. Standard approaches to temporally modeling signaling networks of genes and proteins, such as approaches based on ODEs or traditional stochastic algorithms, do not account for intracellular spatial heterogeneity such as might arise from cellular organization or reaction-diffusion systems (Vilar, et al. 2003). This project, I built a whole-cell spatial stochastic reaction-diffusion toy model of lactose-induced activation of the lac operon, a well-studied example of prokaryotic transcriptional regulation. I used the MCell+CellBlender package (Stiles, et al. 1996; Stiles & Bartol, 2001; Kerr, et al. 2008) to simulate the transport and diffusion of particles directly involved in repression and activation of the lac operon and qualitatively evaluated the resulting macroscopic system dynamics. The results of this preliminary study suggest interesting avenues for further investigation, including the robustness of the lac operon switching system to various noise sources, the sensitivity of this system to various parameter estimates and modeling assumptions, and the difference in time scales between various processes at various spatial scales.
Background
Mathematical and computational modeling of the dynamics of biological systems, ranging in complexity from genetic circuits to entire cells, is an active area of research. Standard approaches to temporally modeling signaling networks of genes and proteins, such as approaches based on ODEs or stochastic algorithms, do not account for intracellular spatial heterogeneity such as might arise from cellular organization or reaction-diffusion systems (Vilar, et al. 2003).
The lac operon is a classic example of prokaryotic transcriptional regulation. Because it is so well-studied, it is useful in developing and evaluating modeling approaches. Expression of enzymes to transport and catabolize lactose is repressed and promoted by transcription factors LacI and CRP, respectively, in response to presence of lactose and absence of glucose (Vilar, et al. 2003). Biochemical models of the lac operon assume spatial homogeneity of the molecules involved, because the small size of prokaryotic cells suggests that even slowly diffusive molecules can reach interaction sites in relatively short times (Soh, et al. 2010). However, important questions remain about the role of diffusion and space, such in the facilitated diffusion of transcription factors (Wunderlich & Mirny, 2008), and in the effects of spatial organization and molecular crowding on reaction kinetics (Roberts, et al. 2011). Recently, a stochastic, coarse-grained spatial model has been developed to investigate reaction-diffusion behavior of LacI in a crowded cellular environment (Roberts, et al. 2011). A reaction-diffusion model of other molecules involved in the lac operon system may better capture some nuances of this system than existing models.
Scope
This project aims to build a whole-cell reaction-diffusion toy model of lactose-induced activation of the lac operon. The model will include repression of the lac operon by LacI and expression of the LacY and LacZ genes, leading to transport of lactose into the cell by lactose permease and degradation of lactose by β-galactosidase, respectively. The toy model will make ballpark estimates for diffusion coefficients and enzyme kinetics when experimental figures are unavailable. Qualitative behavior of the model in various experiments will be evaluated.
Achievements
I could not generate a mesh for a rod-shaped cell with hemispherical polar endcaps that yielded error-free simulations, so I simplified cell geometry to a cylinder with diameter 1um and length 3um. I then generated a box around this cell with walls as concentration clamps to maintain constant concentration of lactose in the cell’s surroundings.
I implemented diffusion of lactose across the cell membrane and transport of lactose by lactose permease as unimolecular and bimolecular reactions, respectively. Then, I implemented catabolism of lactose by beta-galactosidase as a bimolecular reaction. For both proteins, I added reactions for slow protein degradation. I also added a unimolecular reaction for lactose permease in the cytoplasm to attach to the membrane.
To represent expression of LacY and LacZ genes, I made lac operon particles. These particles can undergo a unimolecular reaction creating lactose permease and beta-galactosidase. Alternately, an active LacI particle can bind to a lac operon particle to repress it. To compensate for MCell’s inability to model superdiffusive motion in LacI, I put multiple lac operon particles into the cell, such that near-simultaneous binding and unbinding events in different lac operon particles could stand in for rapid binding and unbinding on a single lac operon in a real cell.
Finally, I implemented reversible binding of LacI particles to lac operon particles, and binding of a single lactose molecule to a LacI particle; this is a simplification from the actual allosteric binding of lactose to LacI. My representation of this process included different binding affinities of LacI to the lac operon and lactose-LacI complexes to the lac operon.
Analysis
The MCell+CellBlender package that I used to simulate the cell is a particle-based Monte Carlo simulator. At every time step, MCell computes velocities and probabilities of reactions based on the locations and orientations of particles with respect to each other and with respect to solid objects. As a particle-based simulator, MCell is more appropriate than continuum-based simulators for experiments involving low-concentration particles, such as LacI and lactose.
I found that the actual threshold concentration at which lactose induces gene expression required too many particles to simulate and animate quickly. Additionally, because all rate constants found in literature were so small that observing changes would require impractically long simulations using short time steps, I increased the rates of most processes, the interaction radius threshold for evaluating reactions probabilities, and the concentration of low-concentration particles such as LacI and the lac operon.
After adjusting model parameters and initial conditions to achieve qualitatively reasonable behaviors, I conducted four simulation experiments and plotted particle numbers, specifically of beta-galactosidase, unrepressed lac operon, LacI unbound to lactose, lactose, and membrane-bound lactose permease, over the course of each simulation. My standard initial conditions (Fig. 1). included lactose at a low concentration of 10 nM (corresponding to ~14 lactose molecules), representing lactose that may have previously diffused into the cell; 15 beta-galactosidase particles, 40 membrane-bound lactose permease molecules, and 40 lactose permease molecules in the cytoplasm that have not yet bound to the membrane, representing lac operon products expressed at a low “leaky” rate; 100 free-floating LacI particles (which do not degrade); and 10 lac operon particles, initially repressed by attached LacI particles. Simulating this cell, without any external lactose, led to eventual catabolism of lactose, along with some leaky expression of the lac operon genes, and stability of particle concentrations (Fig. 2). These results are biologically intuitive, and the noisiness of the system resembles the noisiness of other low-concentration stochastic reaction simulations that do not model diffusion.

Cell with representative initial conditions. Large black spheres represent repressed lac operon particles, and they turn white in absence of repression. Green spheres represent unbound LacI, blue spheres represent beta-galactosidase, pink particles represent lactose permease, and white particles represent lactose. The black box represents the bounds of the system, while the transparent cylinder represents the cell.
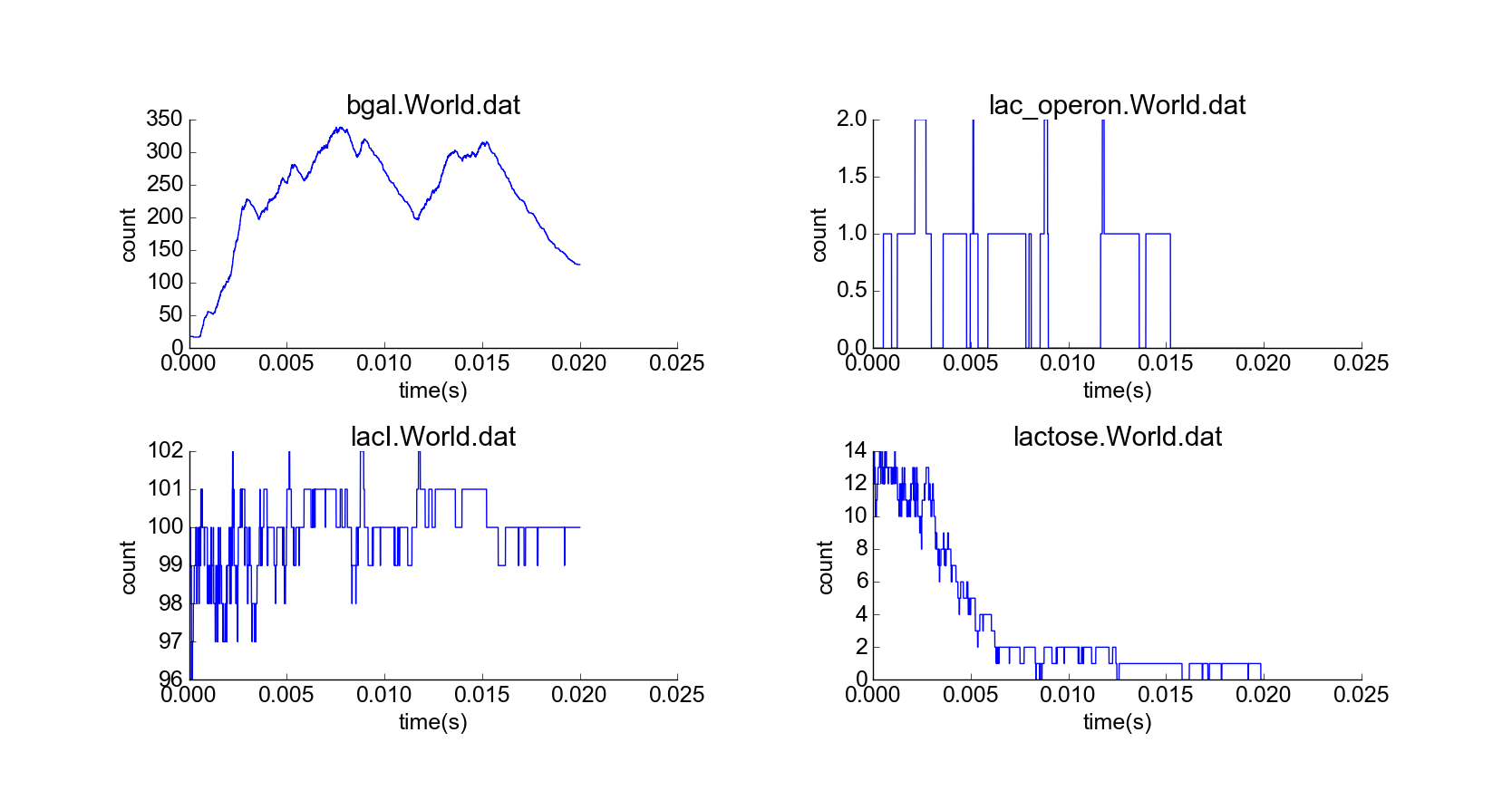
Simulation of cell over 20,000 time steps (1 us per step) from representative initial conditions.
Next, I simulated a cell with an initial lactose concentration of 10 uM in the cytoplasm (Fig. 3). At first, the lactose bound to most of the LacI particles, and the lac operon particles were mostly active, leading to high production of beta-galactosidase, which then catabolized all the lactose particles, leading to repression of the lac operon particles and decrease in the concentrations of their protein products (Fig. 4). The model thus exhibits negative feedback in the absence of external lactose, and this feedback looks physically realistic. Furthermore, a time delay between induction of the lac operon and appearance of lactose permease in the cell membrane emerges from the simulation of diffusion of newly-synthesized lactose permease to the cell membrane, which also makes sense.

Cell with representative initial conditions and initial high lactose concentration (10 uM) in cytoplasm. Note the higher concentration of white spheres, representing lactose molecules.
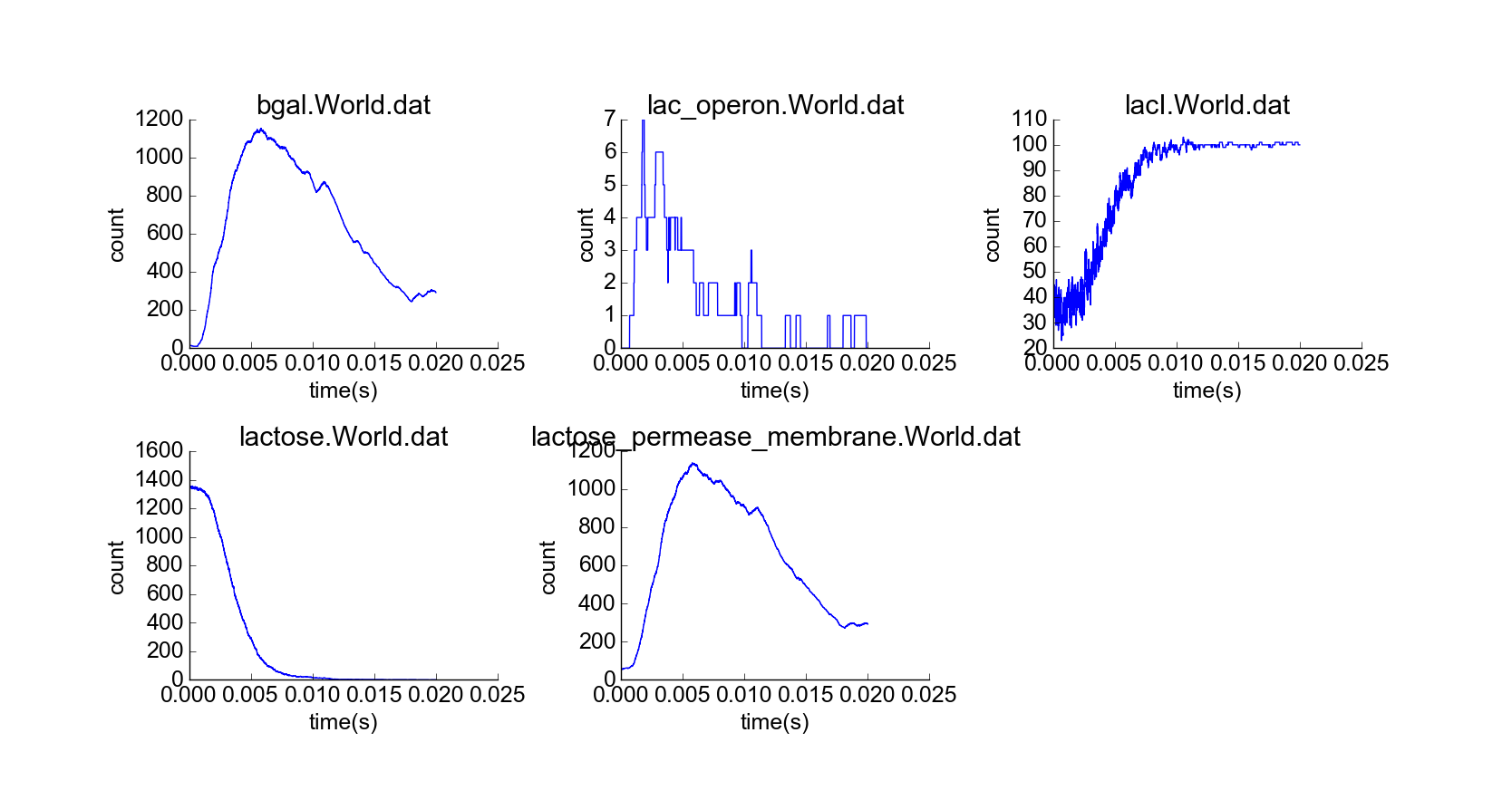
Simulation of cell over 20,000 time steps, initial high lactose concentration.
With confirmation that the toy model reproduces the qualitative behaviors of the lac operon in the absence of external lactose, I then simulated the cell under the initial conditions of the first experiment, but with a constant high extracellular concentration of lactose (Fig. 5). The concentration of lactose seems to increase linearly by transport through lactose permease until the lac operon is induced; then beta-galactosidase and lactose permease appear rapidly, and the concentration of lactose increases exponentially while the concentration of LacI not bound to lactose decreases (Fig. 6). The model thus captures the essential features of positive feedback in the presence of extracellular lactose. The curves look physically realistic, and they capture the noisiness expected for low-to-medium-concentration particles. Longer simulation shows that the system quickly reaches steady state, with lactose concentration relatively robust to noise in the system arising from the low concentration of lac operon particles (Fig. 7). Thus, the system exhibits stability in the absence of external perturbations, perhaps enforced by negative feedback from beta-galactosidase.

Representative early frame of cell simulation with constant high extracellular lactose concentration (10 uM) and standard initial conditions. Yellow particles represent extracellular lactose.
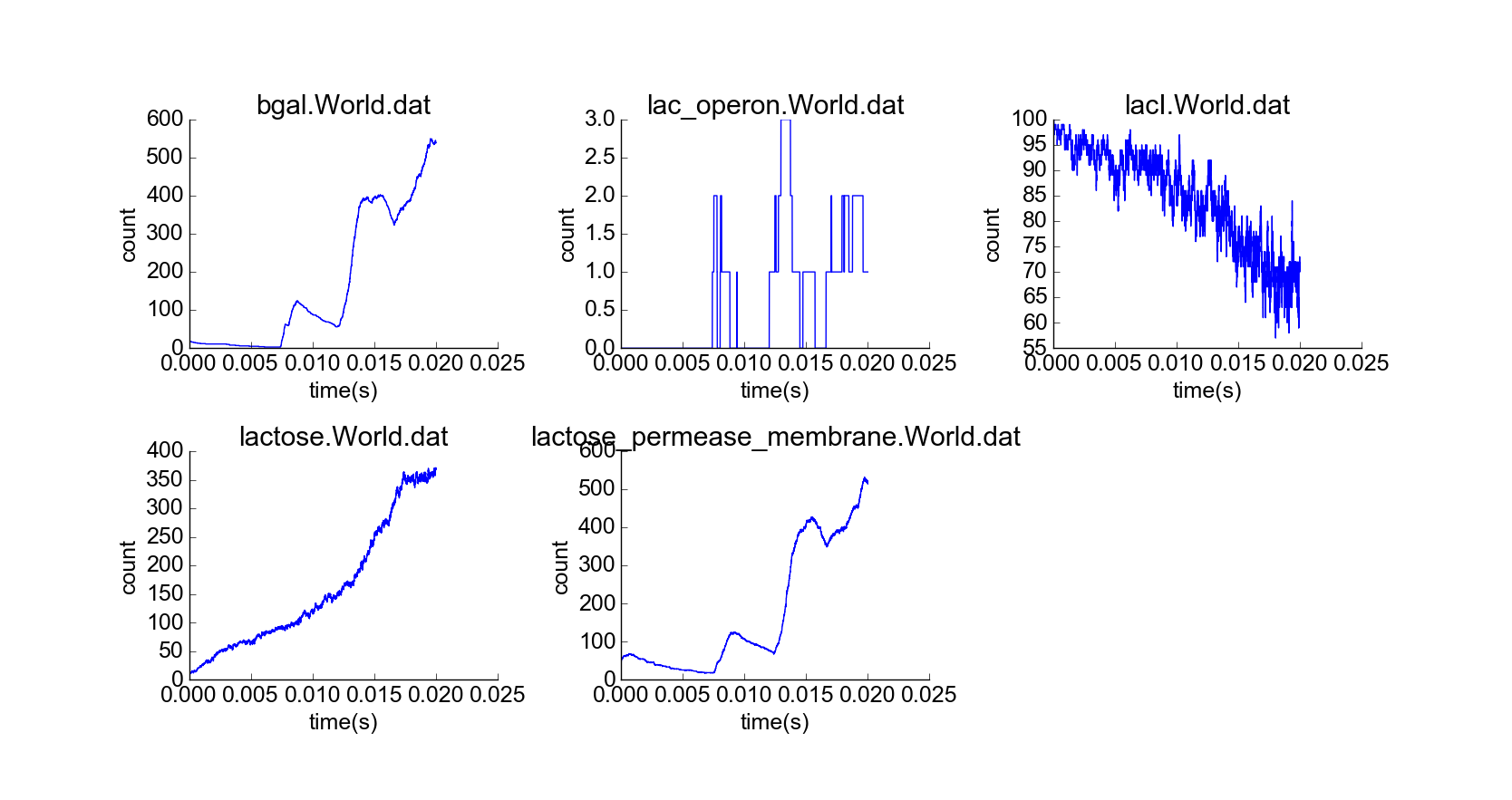
Simulation of cell over 20,000 time steps, constant high extracellular lactose concentration.
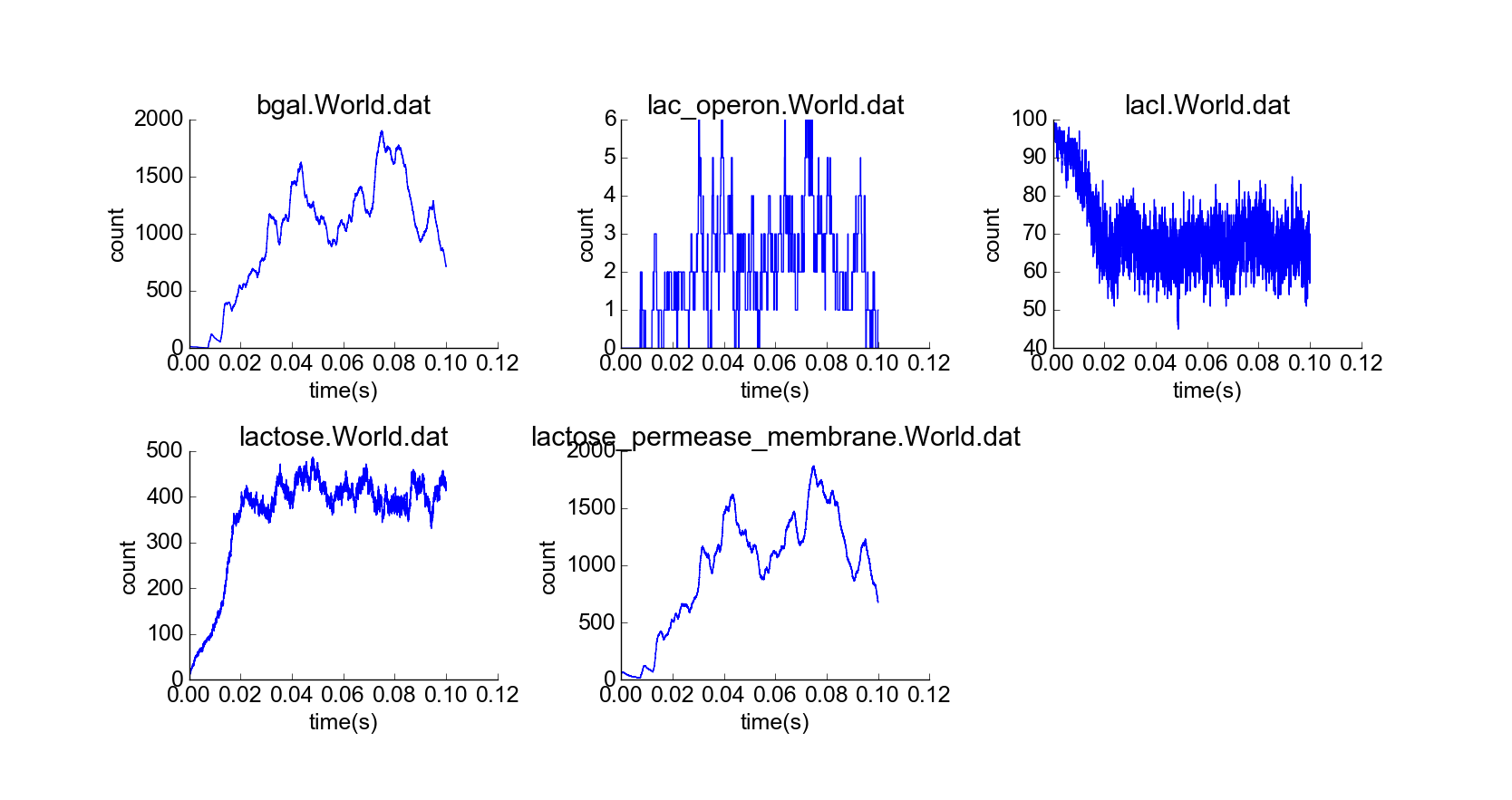
Simulation of cell over 100,000 time steps, constant high extracellular lactose concentration.
Conclusion
This project’s toy model demonstrates the feasibility of using a spatial particle-based reaction-diffusion simulator to investigate the role of stochastic particle transport and low particle concentration in gene and protein network dynamics. From the process of developing the model and the experiments I ran with it, I found potentially interesting macroscopic properties, such as the lac operon system’s robustness to various sources of noise, its sensitivity to various parameter values and assumptions, and the difference in time scales between various processes at various spatial scales. Next steps include testing whether running simulations with longer time steps allows for the use of more realistic model parameter values and quantitative evaluation of the toy model. Although this toy model may not be sophisticated or accurate enough to answer current questions about the lac operon, it does suggest new questions for investigation.